★小学生の内容ですが、意外と中学生もあやしいと思うので、中学生も読んでくださいね★
さぁ!次は『速さ』です!
例年、『速さ』は小学校6年生で習っていました。しかし今は5年生で習うようになりました。
しかも『単位量あたりの大きさ』の流れで習います。

『単位量』はある程度大丈夫になったわ!

私はまだ『単位量』が・・・
『単位量あたりの大きさ』についてはこちらをご覧ください!
こちらを読んでいただくともっと『速さ』が理解できると思います。
『速さ』
『単位量あたりの大きさ』の流れで習うので、『速さ』も『単位量あたりの大きさ』として見ていきます。
『速さ』とは、『1秒間あたりの距離』または『1分間あたりの距離』または『1時間あたりの距離』です。
『速さ』の『単位』は
- m/s または 秒速~m
- km/h または 時速~km
中学生なら『m/s』『km/h』と表しますが、小学生は『秒速~m』『時速~km』と表す方が多いと思います。
どちらにしても
- 『m/s』『秒速~m』であれば、『1秒間経過したときに進む距離(m)』
- 『km/h』『時速~km』であれば、『1時間経過したときに進む距離(km)』
という形になり、『単位量あたりの大きさ』と同じモノになります。
『速さ』を求める問題
100mを16秒で走った時の速さを求めましょう。
『速さ』とは、『1秒間あたりの距離』です。
と、言うことなので『秒』を割算の後ろにおきます。
100(m)÷16(秒)=6.25(m/s)
答えは、秒速6.25mとなります。
320kmを5時間で進む列車の時速を求めましょう。
『時速』ということなので同じく『速さ』!『時速』は『時』という言葉あるので『1時間あたりの距離』です。
ということなので、『時間』を割算の後ろにおきます。
320(km)÷5(時間)=64(km/h)
答えは、時速64kmとなります。
距離を求める問題
秒速6mで10秒間走った距離(道のり)を求めましょう。
秒速6mとは『1秒間に6mを進む』ということです。
1秒で6mなので、10秒だと・・・10倍ってことですね!
秒速6m×10(秒)=60(m)
高速道路を時速80kmで、1時間30分(=1.5時間)走行した距離を求めましょう。
時速80kmとは『1時間に80kmを進む』ということです。
1時間で80kmなので、1.5時間だと・・・1.5倍ってことですね!
時速80m×1.5(時間)=120(km)

私の愛車は高速道路では時速80kmくらいなので
東京ディズニーランドまではノンストップで1時間半くらいかなぁ!
時間を求める問題
学校まで5kmを自転車で時速15kmで走る時間を求めましょう。
時速15kmとは『1時間に15kmを進む』ということです。
1時間に15kmなので、5kmは1/3【5(km)÷15(km)=5/15=1/3】の距離になります。
距離が1/3なので時間も1/3倍して下さい。
1(時間)×1/3=1/3(時間)

1/3時間って???
1/3時間とは、1時間を3つに分ければいいです!
ということは・・・20分ですよね!
高速道路を時速80kmで600km走った時の時間を求めましょう。
時速80kmとは『1時間に80kmを進む』ということです。
1時間に80kmということは、600kmは7.5倍【600(km)÷80(km)=7.5】の距離です。
距離が7.5倍なので、時間も7.5倍にして下さい。
1時間×7.5=7.5(時間)

さぁ、600kmはどこまでの距離でしょう!

600kmはUSJまでの距離です!

USJまで7.5時間かかります・・・
USJ行ったことないので行ってみたいのですが、遠い・・・
と、それはさておき
これらは『単位量あたりの大きさ』を利用した解き方になります。
必殺技の伝授
基本的な概要、考え方については『単位量あたりの大きさ』を基に解いてほしいのですが
ここで昔からずっとある必殺技を伝授します。

それが『み・は・じ』です!
『き・は・じ』または『は・じ・き』で習った方もいらっしゃると思います。
- 『み』は『道のり』(または、『き』は『距離』)
- 『は』は『速さ』
- 『じ』は『時間』
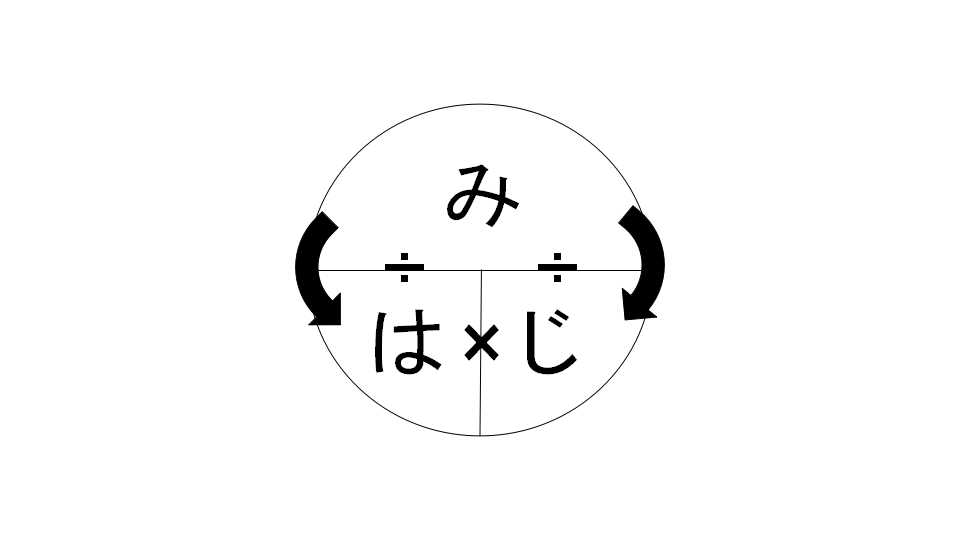
こんな図ですよね!(割算の場合は矢印の順番に割算をします。)
速さを求めたければ・・・
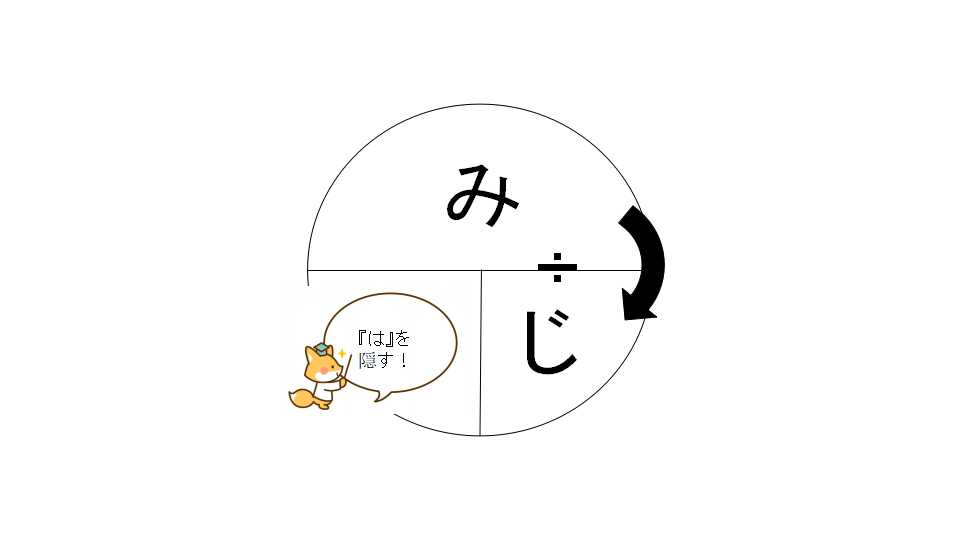
距離(道のり)を求めたければ・・・
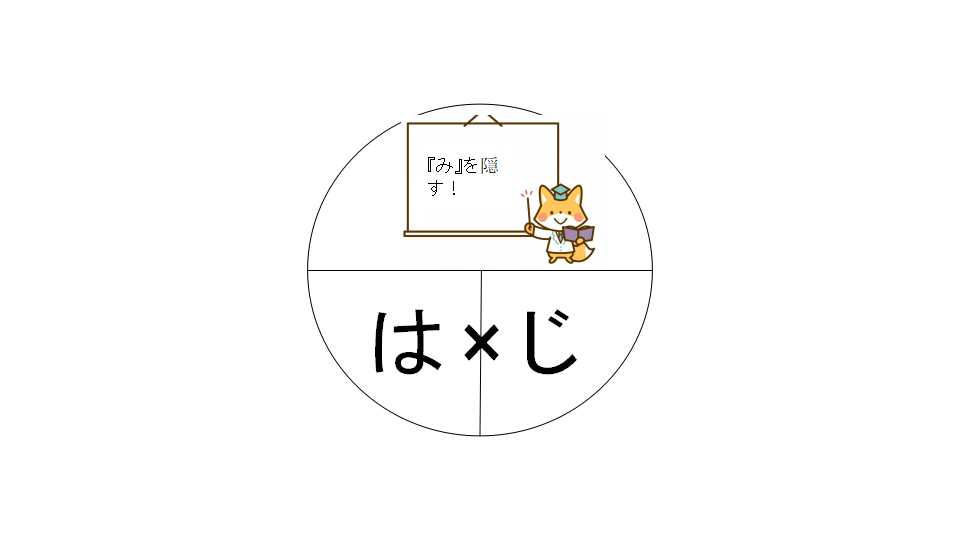
時間を求めたければ・・・

上記図に当てはめれば簡単に解くことが出来ます。

ただ、単位には注意してくださいね!
※単位についてはまた後日お話をします。
まとめ
はい!いかがでしょうか。
最後にお子様への教え方ですが・・・
お子様への教え方
学校で教わっていなかったとしても『み・は・じ』で教えてしまった方がよいと思います。
その際には、お子様に『み・は・じ』の図を描かせて、

求めたいものを指で隠してみて!
そうすると何算をしないといけないかなぁ?
このくらいにしておきましょう!あとは・・・

し~・・・
すべてを教えてしまうと『思考力』が付きません。
単位を変えなければならない問題については、また後日アップします。もしばらくお待ちください。
小学校5年生は、前回の『単位量あたりの大きさ』、今回の『速さ』、そして今ブログ作成中の『割合』がネックとなります。
正直、小学校の算数の中で一番の大変なところです。
ご自宅でも少しでも多く問題を解いていただきたいと思います。







コメント