では、『算数講座(単位量)』よりもネックになる『割合』のお話をします。
『割合』は・・・

掛け算?割り算?
と、どちらで計算をしたらよいのか?定まらない子が多く、計算が得意な子でもつまずく分野です。

私もわからないわ!
教えられな~い!!

『割合』ってわかる?
・・・えっ!?
大丈夫です!簡単ですよ!
少しずつお話をしますね!
『割合』とは?
よく目にするのが
- 30%引き
- 4割引き
とお買い物をする際に値札についているのではないでしょうか!
例えば・・・
アウトレットで、ジャケットが6,000円で売っていたとしましょう!
タイムセールで30%引きになりました。
さて、いくらになるでしょうか?(消費税は考えません。)
考え方は様々あります。
考え方①
6,000円の30%分がいくらかをまずは計算する。
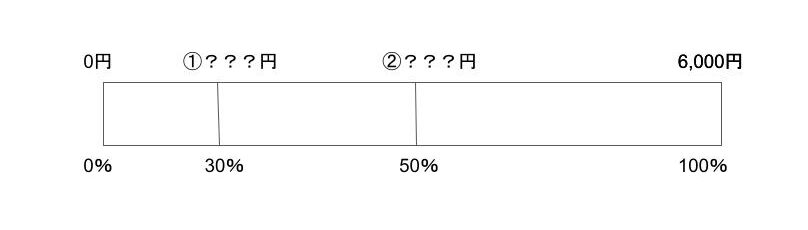
と、その前に簡単な6,000円の50%分から見ていきましょう!
上図のように『割合』はもとにする金額(6,000円)を100%(または‟1”)とします。
そして、50%(または‟0.5”)となると半分なので、50%分は3,000円とわかります。
その際の計算は、6,000×0.5=3,000 です。
※50%では計算ができません。0.5で計算をします。
これと同様に30%も考えましょう!
50%だったから、6,000×0.5=3,000 でした。
30%なら、6,000×0.3=1,800 です。
『30%引き』とは、単純に30%分(今回は1,800円)を引けばいいのです。だから、6,000-1,800=4,200(円)となります。
考え方②
お買い物の際に、考え方①のように計算はしないと思います。
では、どうするか!簡単です!
30%引きということは、残りが70%ということです。
なので、0.7を掛ければ終わりです。6,000×0.7=4,200(円)
これはお買い物の際に直ぐに使えると思います!
『割合』の基礎
いきなりちょっと難しいところをやりましたが、もう一度基礎に戻ります。
まず、この『割合』の分野で悩まされるのが公式となっているモノです。
- 『比べられる量』÷『もとにする量』=『割合』
- 『比べられる量』÷『割合』=『もとにする量』
- 『もとにする量』×『割合』=『比べられる量』
これらを覚えても、どれが『比べられる量』で、どれが『もとにする量』で、どれが『割合』なのか・・・
子供たちにとっては、文章を読んで区別することがなかなかできません。

比べられる量?もとにする量?割合?
『割合』の言葉の区別
まず言葉の区別をしましょう!これができないと、計算ができません。
区別の際に、『もとにする量』と『割合』をまずは見つけましょう!
『もとにする量』とは?
言葉の通り、『もと』です。

もと?
要するに『基準』とか『全体』とかと考えるといいかもしれません。
① 500円の10%は、50円です。
② 60kgの3割は、18kgです。
③ 600mLは、1Lの60%です。
④ 300ページは、250ページの1.2倍です。
簡単な上記文章を見たときに、『もとにする量』がどれかわかりますか?
①は500円、②は60kg、③は1L、④は250ページです。
大人ならば基準が分かると思うのですが、子どもはそれが難しい・・・
ということで、キーポイントは・・・『の』の前です!
① 500円の10%は、50円です。
② 60kgの3割は、18kgです。
③ 600mLは、1Lの60%です。
④ 300ページは、250ページの1.2倍です。
・・・『の』~という文章がとにかくよく出てきます。
『の』の前の・・・にあたる部分が『もとにする量』です。
『割合』とは?
『割合』を見分けるコツは、単位です。
① 500円の10%は、50円です。
② 60kgの3割は、18kgです。
③ 600mLは、1Lの60%です。
④ 300ページは、250ページの1.2倍です。
上記のような単位が付いていたり、単位がなれば、それが『割合』です。
だからこそ、『割合』は見つけやすいと思います。

これならぼくでも!
区別しずらいのは、『もとにする量』と『比べられる量』です。この二つは、単位が同じです。
ただ、上記のように『の』を見つけられれば、『もとにする量』は見つけられます。
『比べられる量』とは?
正直、これを探すよりは、『もとにする量』や『割合』を見つけ、残りが『比べられる量』って見た方が良いかもしれません。
『割合』計算方法
『割合』の言葉の区別が出来たら次は、計算方法です。
ここでも、

掛け算?割り算?
ってなりますよね!
でも、言葉の区別ができればあとは簡単です!
『速さ』の時と同じように次の図を使います。

『く・も・わ』です!
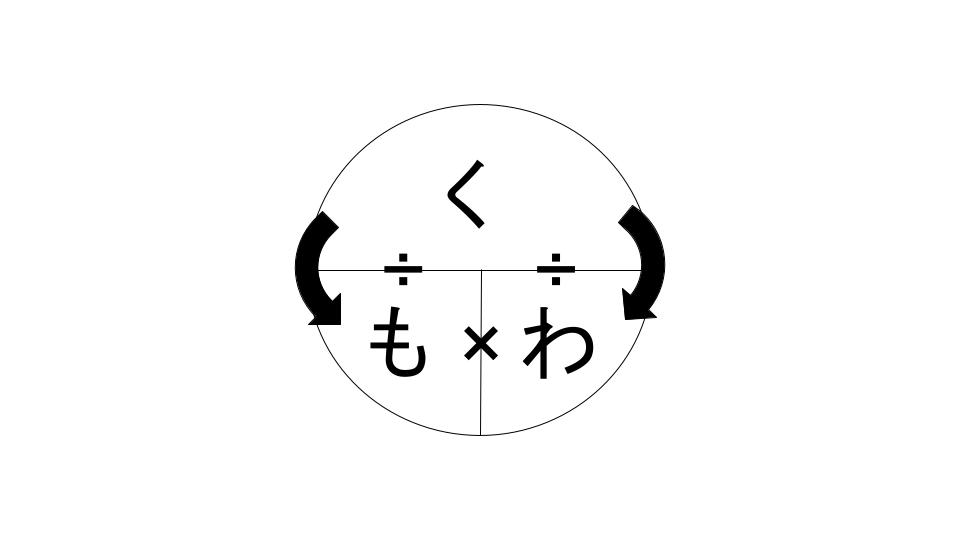
- 『く』は『比べられる量』
- 『も』は『もとにする量』
- 『わ』は『割合』
『もとにする量』を求めたければ・・・
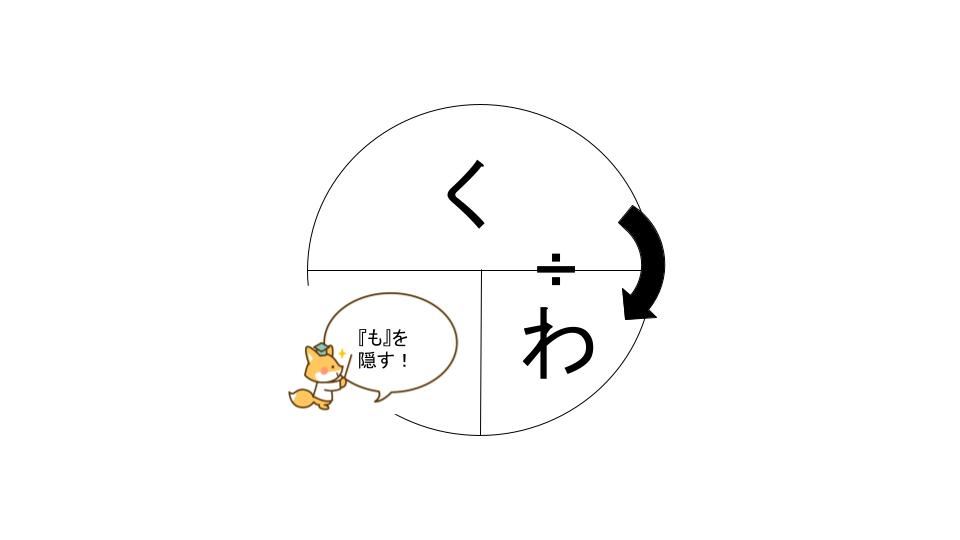
『割合』を求めたければ・・・
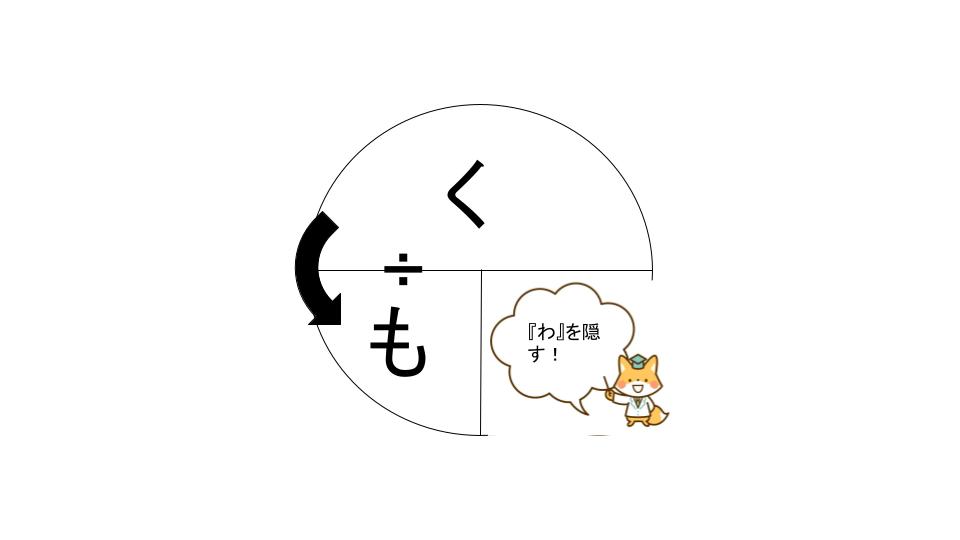
『比べられる量』を求めたければ・・・
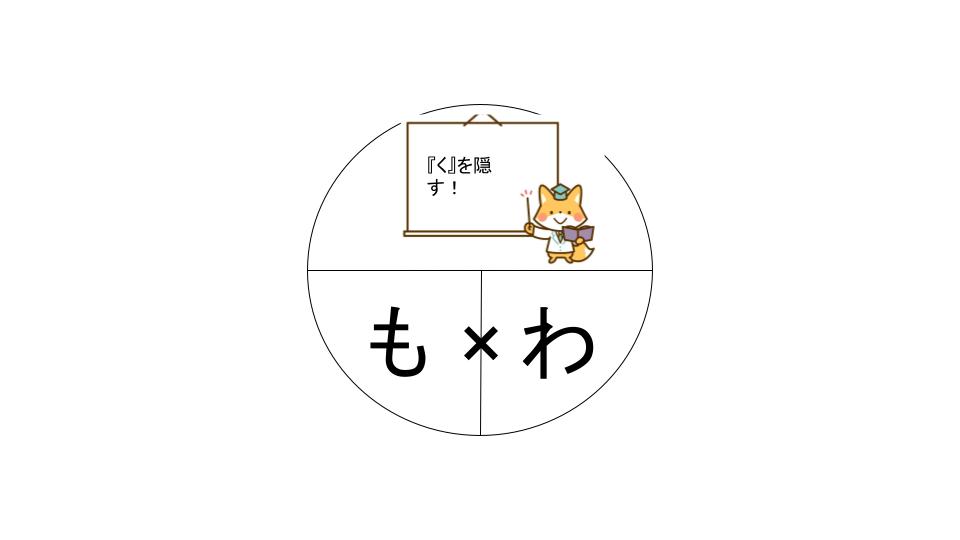
これで『割合』もこわくありませんよね!
まとめ
今回は、『割合』の基礎的な部分にしました。応用編はまたの機会にします。
そして・・・
お子様への教え方
学校で教わっていなかったとしても『く・も・わ』で教えてしまった方がよいと思います。
まずは、『割合』の言葉の区別です。

どれが『もとにする量』かな?

じゃあ、次に『割合』はどれかな?
このくらいにしておきましょう!
そして、お子様に『く・も・わ』の図を描かせて、

求めたいものを指で隠してみて!
そうすると何算をしないといけないかなぁ?
このくらいにしておきましょう!あとは・・・

し~・・・
今回の『割合』が過ぎれば、小学校の算数の大変な分野は終わります。
正直、6年生の方が楽かもしれません。
その分、6年生は英語に時間を費やした方がよろしいと思います。
という形で、『割合』の基礎を終わりにしたいと思います。






コメント